بێکۆتا: نهێنییەکانی و تایبەتمەندییە دەرئاسا و سەرسووڕهێنەرەکانی
Sunday, 19/05/2024, 21:26
"ئەوەی زۆر سەرسامم دەکات لەبارەی ئاستی هۆشمەندی مرۆڤەوە، ئەوەیە چۆن دەتوانین لە شتانێک تێ بگەین کە ناتوانین لە مێشکماندا وێنای بکەین" زانای فیزیک لیڤ لانداو
میوانخانە بێکۆتاکەی هیلبەرت
بهێنینە بەرچاومان میوانخانەیەکمان هەیە بە 100 ژوور و هەمووشیان گیراون، ئەگەر میوانێکی نوێمان بۆ بێت ئەوا ناتوانین وەری بگرین. لەبەرئەوەی میوانخانەکەمان زۆر خۆش و پەسندە، هەڵ دەستین بە زێدەکردنی چەند ژوورێک، پاشان دیسانەوە سەرجەم ژوورەکان پڕ دەبن و پێمان ناکرێ جێ بۆ میوانانی دیکە بکەینەوە. دواجار بۆ ئەوەی بەتەواوی کێشەی کەمی ژوور چارەسەر بکەین، دێین بێکۆتا لە ژووری نوێ بۆ میوانخانەکەمان دروست دەکەین، کەچی دەبینین بە ماوەیەک هەر هەموو ژوورەکان دەگیرێن لەلایەن بێکۆتا لە میوانەکانمان. ئێستە ئەگەر میوانێکی نوێمان بۆ بێت، دەبێ چی بکەین؟
با بڵێین هەر ژوورێک میوانێکی تێدایە و ژمارەمان بۆ ژوورەکان داناوە بەم شێوەیە {1، 2، 3، 4، 5، ....}. بە بیرکردنەوەیەکی سادە پێمان وایە میوانخانەکەمان تەواو جێی هیچ کەسێکی دی تێدا نابێتەوە، بەڵام میوانخانەکەی ئێمە بێکۆتا ژووری هەیە، بۆیە دەتوانین ژوورێک دابین بکەین بۆ میوانە نوێیەکەمان. بەوەی میوانی ژووری 1 دەنێرینە ژووری 2 و ئەوەی ژووری 2 دەگوێزینەوە ژووری 3 و ئەوەی 3یەمیش بۆ ژووری دوای خۆی و ...هتد. بەم شێوەیە بەبەردەوامیی، بەمەش ژووری ژمارە 1 بەتاڵ بوو بۆ میوانە نوێیەکە، کەواتە چەندەی میوانی نوێمان بۆ بێت ئەوا هەر دەتوانین ژوورێکی بۆ دابین بکەین لە میوانخانەکەماندا. ئەگەر 100 میوانی نوێشمان بۆ بێت، ئەوا میوانی ژووری ژمارە 1 دەگوێزینەوە بۆ ژووری ژمارە 101 و ئەوەی ژووری ژمارە 2ش بۆ ژووری ژمارە 102 و بەم شێوەیە شوێن بۆ 100 میوانی نوێ دەکەینەوە، ئەم شێوازە بەکار دەهێنین بۆ ژمارەیەکی سنووردار لە میوانی نوێ.
ئەوەی گەلەک سەیر و سەرسووڕهێنەرە، هیلبەرت دەڵێت: دەتوانین ژمارەیەکی بێکۆتا لە میوانی نوێ لە میوانخانەکەماندا وەربگرین، بەجۆرێک ئەم جارەیان میوانی ژووری 1 ببەینە ژووری 2، میوانی ژووری 2 بۆ ژووری 4، میوانی ژووری 3 بۆ ژووری 6، واتە بەگشتی میوانی ژووری ژمارە n بگوێزینەوە بۆ ژووری ژمارە n2، بەمەش تێکڕای ژوورەکانی ژمارەیان تاکە {1، 3، 5، 7، ....} بۆمان بەتاڵ دەبن، دەرەنجام دەبینە خاوەنی ژمارەیەکی بێکۆتا لە ژووری بەتاڵ بۆ ژمارەیەکی بێکۆتا لە میوانی نوێ. لێرەدا هەموو میوانێک دەتوانێت ژوورێک بگرێت و پێویست ناکات پێشەکی داوای گرتنی ژوورێک بکات لە میوانخانە بێکۆتاکەمان.
ئینجا خۆشییەکەی ئەم میوانخانەیەمان ئەوەیە، ژوورەکانمان زۆر جوانن و خزمەتەکەمان یەکجار باشە و چیت بوێ پێتی دەدەین و لەڕادەبەدەریش هەرزانە، لەبەرئەوەی ئەگەر هەر میوانێکمان یەک دۆلار بدات، مانای ئەوەیە خاوەنی بێکۆتاین لە دۆلارین و هیچ کەسێک هێندەی ئێمە دەوڵەمەند نەبووە لە مێژووی مرۆڤایەتیدا.
بەمە و چەند نموونەیەکی سەرنجڕاکێشی دیکە، دەکارین شیکاری دژبەیەکییەکان بکەین و تایبەتمەندییە نامۆ و ناوازەکانی بێکۆتا لە درێژەی بابەتەکەماندا بخەینە ڕوو.
پێناسەی بێکۆتا
بێکۆتا (Infinity)، برێتییە لە بیرۆکەیەک، یاخۆ چەمکێک کە گوزارشت دەکات لە شتێکی بێسنوور، یان ئەو شتەی تەواو نابێ و هەرگیز ناتوانین بگەین بە کۆتایییەکەی. ئەم وشەیە بە گەلەک واتای جیاجیا بەکار دەهێندرێت، بەڵام بیرۆکەیەکی هاوبەش کۆیان دەکاتەوە ئەویش، نەبوونی دوایییە.
زانای ماتماتیک جۆن واليس (John Wallis)، لەساڵی 1655دا هێمای (∞) بۆ بێکۆتا دادەنێت، دەشێ لە ژمارە 1000ی ڕۆمانیایی (CIƆ، یاخۆ CƆ) کە هەندێ جار بە مانای (زۆر)، یانژی لە ئۆمێگا (ω)ی دوا پیتی گریکییەکانەوە وەرگیرابێ.
زۆرینەی خەڵکی ئاسایی، بێکۆتا بە شتێکی یەکجار گەورە و مەزنی دەبینن کە بەرهەست نییە و ناتواندرێ چییەتی دیار بکرێت، لەوانەیە لەلایاندا یەکسان بێت بە ژمارەی ئەستێرەکان، یان ژمارەی دەنکە لمی لێوار دەریاکان، یاخۆ ژمارەی تێکڕای ئەو مرۆڤانەی هەتا ئەمڕۆکە لە سەر زەویدا ژیاون.
بێکۆتا لە کۆنەوە یەکێکە لە چەمکە هەرە نامۆ و دژوارەکان بۆ زاناکان و فەیلەسووفانیش، چونکە شتێکە زۆر سەختە لە سروشتی ڕاستەقینەدا بدۆزرێتەوە، هاوکات وەک بیرۆکەیەکیش ناتوانین لە مێشکماندا وێنای بکەین. لەبەرئەوەی ئێستا بووەتە چەمکێکی سەرەکیی لە فەلسەفە و ماتماتیک و زانستەکانی دیکەش، بۆیە وامان لێ دەکات بپرسین: بێکۆتا چییە و لەبەرچی لە کۆندا ببووە هۆکاری گرفت و مشتومڕی نێوان زانا و فەیلەسووفان؟ پاشان ئاماژە دەدەین بە تایبەتمەندییەکانی و ڕوونی دەکەینەوە کە چۆن لە پرسێکی کێشەداری زانستییەوە گۆڕا بۆ چەمکێکی ڕیشەیی و بنەڕەتی لە ماتماتیک و فیزیکی هاوچەرخدا؟
جوانترین و ئاسانترین نموونە بۆ شتگەلەکی بێکۆتا لە جیهانی ماتماتیکدا، کۆمەڵە، یاخۆ زنجیرەی ژمارەکانە، ئینجا چی ژمارە سروشتییەکان، تەواوەکان، یان ڕاستەقینەکان و هی دی بێت. ئەو دەمەی ژمارە سروشتییەکان بهێنین و دەست پێ بکەین {0، 1، 2، 3، 4، 5، ....} و هەر بەردەوام بین، ئەوا هەتاهەتایە درێژەی دەبێ و تەواو نابێت. لەبەرئەوەشە پرسیارکردن لەوەی گەورەترین ژمارە کامەیە؟ لە بنچینەوە پرسیارێکی هەڵە و بێمانایە، چونکە تۆ هەر ژمارەیەکم پێ بدەی، من دەتوانم ژمارەیەکی زیادی بخەمە سەر و گەورەتری بکەم. ئەگەر بڵێیت، دەهەزار، ملیۆن، تریلیۆن، گووگل (10 توان 100، لە کاتێکدا ژمارەی گەردیلەکانی گەردوون نێزیکەی 10 توان 80یە)، گووگل پلێکس (10 توان 10 توان 100)، ژماری گراهام و (3)Tree (گەورەترین ئەو ژمارانەن کە بەکار هێنراون لە سەلماندنە ماتماتیکییەکاندا)، دەکارم چەندەم بوێ ژمارەی پتری لەسەر دابنێم، کەواتە لە زنجیرەی بێکۆتادا هیچ ژمارەیەک بوونی نییە، تا ناوی بنێین بە دوا ژمارە. بەم تێگەیشتنەش دەگەینە سەرەکیترین پێناسە، بەوەی کە بێکۆتا لە ماتماتیکدا ژمارە نییە، بەڵکوو چەمکێکی سەربەخۆ و تایبەتییە.
لەگەڵ بوونی ژمارەیەکی یەکجار زۆر لە نموونە لەسەر بێکۆتا، بەڵام دیسانەوە لە کۆندا بۆ هەبوونێکی ڕاستەقینەی ئەم چەمکە، فەیلەسووف و زاناکان ناکۆکییەکی تووندیان لەنێواندا هەبوو. لە لایەنگران، فەیلەسووف ئەناکسیماندەر پێی وابوو بێکۆتا، یاخۆ بێسنوور بنچینە و ڕەچەڵەکی هەموو شتێکە، (ئیکلیدس)یش لە دانانی بەڵگەنەویستەکانی ماتماتیک و ئەندازەدا پشتی دەبەست بە بوونی بێکۆتاکان، هەرچەندە بە ڕاشکاوی نەی دەتوانی ناوی بهێنێت.
بە پێچەوانەی ئەمانە دەبینین بێکۆتاش هاوشێوەی سفر، پیاوانی ئاینی لە ئەوروپادا ماوەیەکی دوورودرێژ دژایەتییان دەکرد و وای بۆ دەچوون کە هێرشێکی ڕاستەوخۆیە بۆ تاکایەتی خوا و سروشتە بێکۆتاکەی، چونکە بەڕای ئەوان تەنیا خوا بێکۆتای ڕەهایە و نابێ شتێکی هاوتای خۆی هەبێ ئەویش بێکۆتا بێت.
لەم ڕوانگەیەوە هەندێک لە زانا و فەیلەسووفان لەو باوەڕەدا بوون، بێکۆتا چەمکێکە دژبەیەک و نالۆژیکیی دروست دەکات، بۆیە ئەستەمە بوونی هەبێت، بۆ ئەمەش چەندان دژبەیەکیی، یاخۆ پارادۆکسیان دەخستە ڕوو بۆ بەلاوەنان و لەناوبردنی بێکۆتا.
دژبەیەکییەکانی زینۆ
لەسەرووی هەمووشیانەوە دژبەیەکییەکانی فەیلەسووفی گریکی دێت کە نێزیکەی 500 ساڵ پێش زاین ژیاوە بە ناوی زینۆی ئێلیایی (Zeno of Elea). زینۆ هاوڕای فەیلەسووف پارمنیدس بوو، بەڕای ئەو جیهانی هەستپێکراو بوونی نییە و تێکڕای شتەکان وڕێنە و ئەندێشەن، نکووڵی لە بوونی کات و شوێنیش دەکرد. ئەم فەیلەسووفە چەندین دژبەیەکی لۆژیکی داهێنا وەک، پێشبڕکێی ئەخیلس و کیسەڵ، دژبەیەکی دابەشکردن، دژبەیەکی تیر و هی دیکەی جۆراوجۆر، ئەمانەش بوونە هۆی ئەوەی زاناکان بەرەوڕووی کێشەیەکی مەزن ببنەوە لەبارەی چەمکی بێکۆتا. زینۆ بە ڕواڵەت پرسیاری ئاسانی دەکرد، بەڵام وەڵامەکان لەڕووی فەلسەفە و لۆژیکەوە گەلەک ئاڵۆز و دژوار بوون.
ناسراوترین دژبەیەکیی لەبارەی دابەشکردنی کات و شوێن، ئەوەیان بوو دەیگوت، گریمان ڕۆژێک بمەوێ لە ماڵەکەمەوە بەرەو باخێکی نێزیک بڕۆم، با بڵێین دووری باخەکە سەد مەتر بێت، دەبێ من یەکەم جار نیوەی دوورییەکە ببڕم (پەنجا مەتر)، واتە یەک لەسەر دووی دوورییەکە (2/1)، پاشان یەک لەسەر چواری دوورییەکە (4/1)، دوای ئەوە یەک لەسەر هەشتی (8/1)، دواتر یەک لەسەر شازدە (16/1)، دواتر یەک لەسەر سیودوو (32/1) و ...هتد. پێویستە هەر بەردەوام بم لەسەر ئەم شێوازە، بەمەش دەبێ ژمارەیەکی بێکۆتا لە بەشەکانی ئەو دوورییە هەنگاو بنێم، کەواتە من ناگەمە باخەکە، چونکە هەتاهەتایە من دەبێ دوورییەکەم بکەمە نیوە. ئاشکرایە بۆ بڕینی دوورییەکی بێکۆتاش پێویستم بە کاتێکی بێکۆتا هەیە، بۆیە من هەرگیز بە باخەکە ناگەم، بەڵام ئەوا من ئێستا لەناو باخەکەم، باشە کردارێک هەنگاوەکانی بێکۆتا بێت، من چۆن توانیم تەواوی بکەم؟ زینۆ دەڵێت ئەمە تەنیا یەک ڕاڤەی هەیە، ئەویش جووڵە ئەندێشەیە و بوونی نییە، ئەگەرچی بۆ هەستەکانمان واش دەرنەکەوێت.
بۆ تێگەیشتنێکی چاکتر، ئەم دژبەیەکییە بەشێوازێکی یەکجار جوان و سەرنجڕاکێش لەم دواییانەدا خرایە ڕوو لەلایەن بیرمەند و فەیلەسووف بێناردێت (José Benardete)، ئەوەی پێی دەگوترێت دژبەیەکی کتێب.
با بڵێین، کتێبێکمان هەیە بە شێوەی چیرۆک، وا دەکەین ئەستووری لاپەڕەی یەکەمی نیو سانتیمەتر بێت، لاپەڕەی دووەمی چارەکە سم، لاپەڕەی سێیەم یەک لەسەر هەشتی سم، لاپەڕەی چوارەم یەک لە شازدەی سم و ...هتد. بەم شێوازە بەرەو بێکۆتا لە ژمارەی لاپەڕەکانی. ئێستا دەپرسین ئەستووری ئەم کتێبە چەندە؟ بۆ وەڵامەکەی دەبێ ئەستووری لاپەڕەکانی کۆ بکەینەوە، بەوەی نیو سم، کۆ چارەکە سم، کۆ یەک لە هەشتی سم، کۆ یەک لە شازدەی سم و هەروەها تا بێکۆتا لە بەشەکان. بە پەنابردنە بەر بنەما ماتماتیکییەکانی تایبەت بە کۆی زنجیرە یەک بەدوای یەکەکان، دەرەنجام دەگەینە ئەوەی کۆی ئەم بەشانە ئەستووری کتێبەکەیە و دەکاتە 1سم. کەواتە ئێمە کتێبێکمان لەبەر دەستە ژمارەی لاپەڕەکانی بێکۆتایە و ئەستوورییەکەشی 1 سانتیمەترە. لێرەدا دەست دەکەم بە خوێندنەوەی کتێبەکە، بەڵام لەپڕێکدا بۆ خۆشی و وەک سەربزێوییەک ویستم سەیرێکی دوا لاپەڕە، یاخۆ دوا دێڕەکانی کتێبەکە بکەم، بۆ ئەوەی بزانم چیرۆکەکە چۆن تەواو دەبێت؟ ئایا دەتوانم شتێکی وا بکەم؟
لەڕاستیدا وەڵامەکە هەم بە بەڵێیە و هەمیش بە نەخێرە! بەڵێ، لەبەرئەوەی کتێبەکە لە دەستمە و ئەستوورییەکەی یەک سانتیمەترە، هەڵی دەگێڕمەوە و دەچمە سەر دوا لاپەڕە و دەی خوێنمەوە بزانم چی هەیە لەدوا دێڕەکانیدا. نەخێر، چونکە کتێبەکەم بێکۆتا لاپەڕەی هەیە، واتە لاپەڕەی کۆتایی نییە و چەندەی لاپەڕە هەڵ بدەمەوە هەرگیز ناگەمە دوا لاپەڕە بۆ خوێندنەوەی کۆتایی چیرۆکەکە. ئاشکرایە وەڵامی بەڵێ و نەخێر بۆ شتێک لەیەک کات و ساتدا دژبەیەکی لۆژیکی دروست دەکات.
بێگومان ئەم دژبەیەکییانە لە ماتماتیکی لکی تەواوکاری و جیاکاریدا (calculus)، دەزانین شیکارەکەی چۆنە و بە سەرنجدانمان لە دژبەیەکی زینۆ، دەبینین ڕاستی دەکرد لەوەی ڕێی چوونە ناو باخەکە لە بێکۆتا بەش، یان ژمارە پێک دێت، بەڵام هەڵەکەی زینۆ لەوەدایە نەی دەزانی کە ئێمە دەکارین ئەو بەشە بچووکانە کۆ بکەینەوە، وەک ئەوەی لە تەواوکاری و جیاکاریدا چارەسەر دەکرێت. بەشەکان هەرچەندە بێکۆتاش بن، درێژی ڕێیەکە بەرە بەرە کەم دەبێتەوە و تا وای لێ دێت گەلەک نێزیک ببێتەوە لە سفر، ئەو دەمە دەکرێ کۆ بکرێنەوە، چونکە بەگوێرەی یاسای کۆکردنەوەی یەک بەدوای یەکە ئەندازەیییە بێکۆتاکان دەرەنجامەکەی دەبێتە ژمارەیەکی تەواو کە دەکاتە یەکەی درێژی ڕێیەکە و یەکسان دەبێت بە 1، بەم شێوەیە: {2/1 + 4/1 + 8/1 + 16/1 + 32/1 ...... = 1}. بەمەش کەسەکە ڕێیەکە هەمووی دەبڕێت وەک ئەوەی تێکڕای بەشەکان کۆ بکاتەوە. ئەوەشمان لەبیر نەچێت، لە چوونمان بەرەو باخەکە، لە بڕینی هەر دوورییەک بەرە بەرە کاتی کورتترمان پێویست دەبێت، یەک لەسەر هەشتی ڕێیەکە نیوەی کاتی یەک لەسەر چواری ڕێیەکەی گەرەکە و ...، بە نێزیکبوونەوە لە باخەکە کاتێکی یەکجار کورتم دەوێ بۆ گەیشتن، لە هەنگاوی دواجاریشمدا پێ دادەنێمە ناو باخەکە. کەواتە گوتەی زینۆ هەڵەیە و کات تێ دەپەڕێت و جووڵەش ڕوو دەدات و هیچیان ئەندێشە و وڕێنە نین.
بۆ بابەتی دژبەیەکی کتێبەکەش، وەڵامی هاوشێوەی باخەکەی زینۆ لە جیاکاری و تەواوکاریدا دەستمان دەکەوێت، بەڵام زۆر بەکورتی ڕاڤە لۆژیکییەکەشی ئەوەیە، ئەستەمە کتێبێک بێکۆتا لاپەڕەی هەبێ، هاوکات چیرۆکێکی بێکۆتاش کۆتایی نەهاتووە و نایەت، تا ئێمە بچین دوا دێڕەکانی بخوێنینەوە.
جۆرج کانتۆر و بیردۆزی کۆمەڵەکان
نموونەکانی پێشوومان بۆ تێگەیشتن بوو لە دژبەیەکی لە بچووک بوونەوەیەکی بێکۆتا، بە پێچەوانەوە دژبەیەکیشمان هەیە بۆ شتە یەکجار گەورە و بێسنوورەکان، هاوشێوەی دژبەیەکە سەیر و سەمەرەکانی زانای ماتماتیکی ئەڵمانیایی فرە ناودار داڤید هیلبەرت (David Hilbert). لە هەمووشیان ناسراوتر دژبەیەکی میوانخانەکەی هیلبەرتە کە لەسەرەتای بابەتەکەماندا ئاماژەمان پێی دا، ئەوەیان ئەزموونێکی ئەندێشەیی بوو بۆ پێناسەکردنی تایبەتمەندییەکی نالۆژیکی کۆمەڵە بێکۆتاکان.
هێنانەوەی ئەم چەند دژبەیەکییانە، بۆ ئەوەیە ببێتە یاریدەرێکی چاک بۆ ڕاڤە و تێگەیشتن لە بێکۆتا و دەستنیشان کردنی تایبەتمەندییەکانی. یەکێک لە سەرەکیترین تایبەتمەندی بێکۆتا وەک گوتمان کە چەمکێکە ئاستی کۆتایی نییە، یاخۆ بێسنوورە، بەڵام دەبێ ئاگەداری ئەوە بین، مەبەست لە بێکۆتا تەنیا شتگەلە قەبارە گەورەکان نییە، چونکە ئەو دەمەی سەیری کۆمەڵەی ژمارە تەواوەکان دەکەین {...، -3، -2، -1، 0، 1، 2، 3، ...}، دەبینین ژمارە ئەرێنییەکان بەرەو گەورەتر و بێکۆتا دەڕۆن، لە هەمان کاتدا ژمارەی نەرێنیشمان هەن کە بەرە بەرە بچووکتر دەبنەوە و هەرگیز کۆتایییان نایەت و زنجیرەکە لە هەردوو ئاراستەوە بێکۆتا درێژ دەبێتەوە. دەشێ ئەمەشیان بەرەو ئەوەمان ببات بڵێین، کەواتە بێکۆتا ژمارەیەکی لەڕادەبەدەر بچووک، یان لەڕادەبەدەر مەزنە، دیسانەوە ئەمە هەڵەیەکی گەلەک گەورەیە بەرانبەر بە بێکۆتا، چونکە چەندان جار ئاماژەمان پێی دا کە بێکۆتا ژمارە نییە، بەڵکوو چەمکە. ئەم جۆرە هەڵەیە لەلای کەسانی خاوەن بڕوانامەی بەرزی زانستیدا بوونی هەیە، لە کۆندا زاناکانیش دووچاری ئەو هەڵەیە دەبوون و کتێبەکانیان پڕ بوو لە بێکۆتا کۆ 1 دەکاتە بێکۆتا، بێکۆتا کۆی بکەیتەوە لەگەڵ بێکۆتا ئەوا دەرنجامەکەی یەکسانە بە بێکۆتا، هەموو ئەمانە وای لە زۆرێک لە زانستمەندان دەکرد، وا تێ بگەن بێکۆتا ژمارەیە. سەرلەبەری ئەو تێڕوانینانە وەک دەربڕینێکی هێمایی دەمێننەوە و ناخرێنە چوارچێوەی بابەتگەلە زانستییەکان، ڕاڤە و شیکاری ڕاستەقینە لە ماتماتیکدا بۆ سەرجەم دژبەیەکییەکانی هاوشێوەی میوانخانەکەی هیلبەرت و ئەوانەی زینۆ، لەڕێی ئەو شتەوە ئەنجام دەدرێت کە ناو دەنرێ بە بیردۆزی کۆمەڵەکان (Set theory).
زانای ماتماتیکی فرە بەناوبانگ جۆرج کانتۆر (Georg Cantor: 1845 - 1918)، داهێنەری تێکڕای بابەتەکانە لەبارەی بێکۆتا کە لێیان دەدوێن، دانەری بیردۆزی کۆمەڵەکان و تایبەتمەندییەکانی بێکۆتایە لە کۆکردنەوە و لێکدەرکردن و دیارکردنی کامە کۆمەڵە گەورەتر، یاخۆ بچووکترە لەوەی دیکە، ئەوانەی لە خوێندنگە و زانکۆکان دەخوێندرێن و بوونەتە بنچینەی ماتماتیکی هاوچەرخ.
بەگوێرەی بنەماکانی بیردۆزی کۆمەڵەکان، ئەو دەمەی وێستێک دەکەین لەو گوتەیەی دەبێژێت، کۆمەڵەیەکی بێکۆتا کۆ کۆمەڵەیەکی بێکۆتا یەکسانە بە کۆمەڵەیەکی بێکۆتا، دەمان بات بەرەو تایبەتمەندییەکی گەلەک نامۆی بێکۆتا، واتاکەی ئەوەیە بێکۆتاکان خاوەن قەبارە، یان بڕن و بە بەراوردکردنی ژمارەی توخم و یەکەکانیان دیار دەکرێن و جیاوازییان لەگەڵ یەکدیدا هەیە.
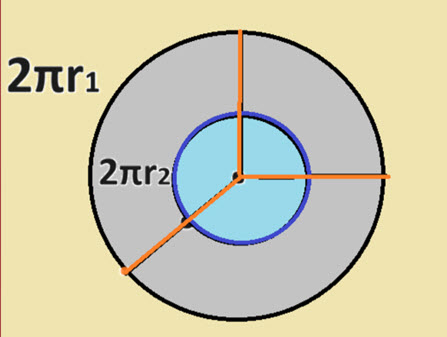
بە نموونەیەک یەکسانبوونی دوو کۆمەڵەی بێکۆتا دەخەینە ڕوو، بەوەی ئێمە دەزانین کە شێوە ئەندازەییەکی وەک بازنە، چیوەکەی هێڵێکە لە ژمارەیەکی بێکۆتا خاڵ پێک دێت. کاتێک بازنەیەکمان هەبێ تیرەکەی 2مەتر بێت و لەناویدا بازنەیەکمان کێشا بە تیرەیەکی 1مەتر، ئاشکرایە چیوەی بازنە گەورەکە (1πr2) گەورەترە لە چیوەی بازنە بچووکەکە (2πr2). بەگوێرەی لۆژیک پێویستە ژمارەی خالەکانی چێوەی بازنە گەورەکە پتر بن لە بچووکەکە، بەڵام وا نییە، چۆن؟
ئەگەر بێین لە چەقی بازنە بچووکەکە کە دەکاتە چەقی گەورەکەش، هەر خاڵێکی بە شێوەی هێڵێک بگەینین بە خاڵێکی سەر چیوەی بازنە بچووکە و درێژی بکەینەوە بۆ چیوەی بازنە گەورەکە، دەبینین سەرجەم خاڵەکانی چیوەی بازنە بچووکەکە بەرانبەرە بە خاڵێکی چیوەی بازنە گەورەکە. کەواتە خاڵەکانی هەردوو بازنەکە یەکسانن، ئەمەش هەرگیز ڕوو نادات ئەگەر ژمارەی خاڵەکانی سەر هەردوو چیوەی بازنەکان بێکۆتا نەبن.
دەبێ لێرەدا ئاگەدار بین، یەکسان واتە هەمان ژمارە لە یەکەکان، یاخۆ ژمارەی توخمەکانی کۆمەڵەکان، چونکە نابێت بڵێین بێکۆتا لە سێو یەکسانە بە بێکۆتا لە هەرمێ، بەڵکوو مەبەستمان ژمارەی ئەو شتانەیە هەر کۆمەڵەیەک لەخۆی دەگرێت.
ئاسایییە نەتوانین لەم تایبەتمەندییە سەیرانە بەئاسانی تێ بگەین، لەبەرئەوەی ئێمە پابەندین بە چەند بەڵگەنەویستێکی ئیکلیدس کە ناسراوترینیان دەبێژێت، "هەمووێک گەورەترە لە بەشێک" ئایا ئەمە دژبەیەکییەک لەگەڵ لۆژیک بەرپا ناکات؟
لەڕاستیدا ڕاڤەی بنەماکە ئەوەیە، دەکارین یەکە بەیەکەی ژمارەی کۆمەڵەکان بەرامبەر یەکیان بکەینەوە بە بێکۆتا.
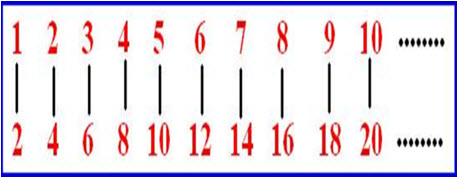
بۆ نموونە، کۆمەڵەی ژمارە سروشتییەکان یەکسانە بە: کۆمەڵەی ژمارە تاکەکان، کۆمەڵەی ژمارە جووتەکان، هەروەها یەکسانە بە کۆمەڵەی ژمارە سەرەتاییەکان، یاخۆ خۆبەشەکان (تەنیا بەسەر 1 و بەسەر خۆیاندا دابەش دەبن).
ژمارە سروشتییەکان: 0، 1، 2، 3، 4، 5، .....
ژمارە سروشتییە تاکەکان: 1، 3، 5، 7، 9، 11، .....
ژمارە سروشتییە جووتەکان: 0، 2، 4، 6، 8، 10، .....
ژمارە سروشتییە خۆبەشەکان: 2، 3، 5، 7، 11، 13، .....
بەڵام کۆمەڵەی بێکۆتای ژمارە سروشتییەکان {0، 1، 2، 3، .....}، بچووکترە لە کۆمەڵەی بێکۆتای ژمارە تەواوەکان {...، -3، -2، -1، 0، 1، 2، 3، ...}، کەواتە لێرەدا کۆمەڵەیەک بێکۆتایە، کەچی گەورەتر، یان بچووکترە لە کۆمەڵەیەکی دی بێکۆتا.
لەوەش سەیرتر کانتۆر دەی سەلمێنێت، ژمارە سروشتییەکان کە بە بێکۆتا دەژمێردرێت، بێکۆتایەکی لەخۆی زۆر گەورەتر خۆی شاردۆتەوە لە نێوان گشت دوو ژمارە بەدوای یەکەکانی وەک 0 و 1، 1 و 2 و ...هتد. باشە ئەمە بۆ؟
چونکە ئەگەرێکی بێکۆتامان لەبەر دەستە بۆ ڕیزکردنی ژمارەکانی دوای خاڵی دەیی {...0.0001242، ...0.2145678، ...0.999970، ...}. ئەمەشیان بە نموونەیەکی دیکە ڕوون دەکەینەوە.
جۆرەکانی بێکۆتا
لەبەر بوونی چەند تایبەتمەندییەکی جۆراوجۆر و جیاجیای بێکۆتا، زانا ماتماتیکییەکان کۆکن لەسەر هەبوونی دوو جۆرە بێکۆتا، یەکیان ناو دەنرێ بە بێکۆتای شیاو بۆ ژماردن، ئەوەی دووەمیان بێکۆتای نەشیاو بۆ ژماردن.
ژمارە سروشتییەکان بە بێکۆتای شیاو بۆ ژماردن دادەندرێن، ئەوەش شتێکی لۆژیکییە، چونکە دەتوانین بیان ژمێرین ئەگەر بێکۆتا کاتمان هەبێت. دەکارین کۆمەڵە مرۆڤانێک بە بێکۆتای شیاو بۆ ژماردن دابنێین (بە بوونی کاتێکی بێکۆتا)، لەبەرئەوەی دەکرێ لیستێک دروست بکەین بە ناوەکانیان، تەواو هاوشێوەی ژمارە سروشتییەکان. بەشێوەیەکی گشتی کۆمەڵەیەکی بێکۆتا لە شتگەلەکان بە بێکۆتای ژمێردراو پێناسە دەکرێت، ئەگەر شتەکانی بۆ ئەوە بشێن کە یەک بەدوای یەک بژمێردرێن.
بۆ تێگەیشتنیش لە بێکۆتای نەشیاو بۆ ژماردن، با بیر لە هێڵێک بکەینەوە لە شێوەی ڕاستەیەکی درێژ، ئەوا پێمان دەکرێ هەر خاڵێک لەو ڕاستەیەدا ژمارەیەکی پێ بدەین. سەرەتای ڕاستەکە بە ژمارە 0 دەست پێ دەکات، لە ناوەڕاستی 1 مەتردا ژمارە 0.5 دادەنێین و ...هتد. ئایا دەتوانین ژمارە بدەینە خاڵەکان و بیان ژمێرین؟ بەڵێ، دەشێ ژمارە بەدوای ژمارە بەرەوژوور ڕیز بکەین. بەڵام لێرەدا تووشی کێشەیەکی نوێ دەبینەوە، بەوەی کە زانیمان ژمارەی یەکەم 0 بوو، ئەی ژمارەی دوای ئەو چەندە؟ ژمارە 0.1 ڕاستە؟ بێگومان نەخێر، چونکە ژمارە 0.01 لەو بچووکترە، ئەی 0.001؟ دیسانەوە نەخێر، هەر کامە ژمارە وەربگرین، دەتوانین ژمارەیەکی بچووکتر بدۆزینەوە، کەواتە دانانی ژمارە و دروستکردنی لیستێک کارێکی نەکراو و ئەستەمە. دەبێ شێوازێکی دیکە نەبێت بۆ چارەسەرکردنی ئەم کێشەیە؟ نەخێر، هەرگیز ناتوانین لیستێک دروست بکەین لە ژمارە ڕاستەقینەکان، بەمەش دەرنجام دەگەینە ئەوەی خاڵەکانی هەر هێڵێک بێکۆتایەکی نەشیاوە بۆ ژماردن.
پاش هەموو ئەمانە چەند جارێکی دەیڵێینەوە کە تێگەیشتن لە بێکۆتا شتێکی ئاسان نییە، بۆیە زۆرینەی زانا و فەیلەسووفانی پێش کانتۆر پێیان وا بوو سەرجەم بێکۆتاکان یەکسانن. ئەم بۆچوونەش لە ڕووی لۆژیکییەوە ئاسایییە، چۆن دەبێ بێکۆتاکان جیاوازییان هەبێت لەگەڵ یەکدی، یانژی بێکۆتایەک گەورەتر بێت لە بێکۆتایەکی دی؟ وەڵامەکەمان ئەوەیە، ئێمە هەرگیز نابێت بڕوانینە بێکۆتا وەک نەدیارێک لە شێوەی ئێکس (X)، یان بچووکتر، یاخۆ گەورەترە لە ئێکس، چونکە گوتمان گشت بێکۆتاکان یەک شت نین و جیاوازن. بەم دەربڕینە جارێکی دی گەیشتینە تایبەتمەندییەکی نامۆ، بەوەی بێکۆتا کەم بێکۆتا یەکسان نابێت بە سفر، لەبەرئەوەی تۆ نازانیت ئایا بێکۆتای یەکەم هەمان بێکۆتای دووەمە؟ دەرنجامەکەی تەنیا ئەوەندەمان پێ دەکرێت ببێژین، بێکۆتا لە بێکۆتا دەر بکەین، بڕێکی نەدیار و نەزاندراومان پێ دەدات، واتە شیکارمان بۆی نییە.
گرینگییەکانی بێکۆتا لە زانستەکاندا
لەڕاستیدا چەمکی بێکۆتا گرینگییەکی زۆری هەیە لە تێکڕای زانستەکان، لە ماتماتیکدا نەک تەنیا تێزێکی ڕیشەیییە، بگرە چەندان لک و بەشی ماتماتیکی لەسەر بنچینەی بیرۆکەی بێکۆتا هاتووەتە دامەزراندن وەک، جەبر و ئەندازە و جیاکاری و تەواوکاری.
لە جەبردا کاتێک ئاماژە دەدەین بە سنووری ژمارەکان و کۆمەڵە جیاجیاکانیان، ناچار دەبین بێکۆتای تێدا بەکار بهێنین، لە کۆمەڵەی ژمارە ڕاستینەکانیش دەبینین دوو جۆرە ژمارەمان هەن، یەکیان ژمارە ڕێژەییەکانە کە دەتوانین بەشێوەی ژمارەیەکی کەرتیی، یاخۆ کەرتدار بیان نووسین، ئەوانەی سەری کەرت و ژێری کەرتیان ژمارەی تەواون، دووەمیانیش ژمارە ناڕێژەییەکانن هاوشێوەی پای و ڕەگی دوو کە لەمانەدا زنجیرە ژمارەکانی پاش کۆما نە چەندبارە دەبنەوە و نە کۆتاییشیان هەیە. لە ژمارەیەکی ئەم جۆرەی ناڕێژەیی کە پێیان دەگوترێت ژمارە گەردوونییەکان، ڕووبەڕووی شتێکی یەکجار نامۆ و سەرسڕکەر دەبینەوە، بەوەی کە هەر ژمارەیەکیان دەتوانێت سەرلەبەری زانیارییەکانی گەردوون لەخۆ بگرێت (لە بابەتێکی سەربەخۆدا لێی دەدوێین).
هاوکات بێکۆتا لە لکی ئەندازەشدا بایەخی گەلەک زۆرە، خاڵ و هێڵ بوونیان نەدەبوو بەبێ چەمکی بێکۆتا، لەبەرئەوەی هێڵ لە ژمارەیەکی بێکۆتا لە خاڵ پێک دێت، واتە سنووری نییە و بە دەربڕینێکی هێمایەکی دەکارین ببێژین کە هێڵ درێژییەکی بێکۆتای هەیە. لە ماتیماتیکدا بەگشتی ئەو دەمەی لە خشتەی تانوپۆدا (یاخۆ پۆتانی دیکارتی) نەخشەی هاوکێشەیەک، یان فەنکشنێکی لە نموونەی ئێکس یەکسان دەبێت بە یەک لەسەر ئێکس {f(x)=1/x}، ئەوا هەر دەبێ پەنا ببەینە بەر بێکۆتا بۆ پێناسەکردنی جووڵەی هێڵە چەماوەکە و بابەتی یەکتربڕین لەگەڵ تەوەرەی ئێکس و وای.
پێشتر گوتمان هەندێ لە دژبەیەکییەکان لە تەواوکاری و جیاکاریدا بەئاسانی چارەسەر دەکرێن، چونکە هەر بیرکردنەوە لە ژمارە یەکجار بچووکەکان و بێکۆتا و دژبەیەکییەکانیشە بووە هۆکاری سەرهەڵدانی ماتماتیکی جیاکاری و تەواوکاری، لە دوا ساڵەکانی سەدەی شازدەیەم لەلایەن دوو زانای فرە بەناوبانگ نیوتن و لەیبنیز. ئەو دوو زانایەش سەرەتا ڕووبەڕووی گەلەک ڕەخنەی تووند و کێشە و مشتومڕی جۆراوجۆر بوونەوە، بەهۆی بیروڕا و کارەکانیان لەگەڵ چەمکی بێکۆتا، بۆیە چەندان جار هەوڵیان دا لە شیکارەکانیاندا جێگرەوەیەک بۆ بێکۆتا بدۆزنەوە، بەڵام هەر سەرکەوتوو نەبوون، تا لە دواییدا بەکارهێنانی بێکۆتا بووە بنەمایەکی سەرەکیی لە کۆمەڵێک بابەتی ماتماتیکی و هی دیکە.
زۆربەمان پێمان وایە، بێکۆتا وەک چەمکێکی ڕاستەقینە بوونی نییە لە سروشتدا، کەواتە لە زانستێکی هاوشێوەی فیزیکیشدا نابیندرێت و تەنیا بەندە بە چەند بابەتێکی ماتماتیکی. دەشێ ئەم بۆچوونە تا ڕادەیەک لە ڕاستییەوە نێزیک بێت، چونکە بێکۆتا لە کۆندا پتر وەک بیرۆکەیەک و پرسێک بۆ گفتوگۆ ناسراو بوو، لەوەی بەکردارەکیی بوونی هەبێت. نیوتن گوتی، هەر دەبێ گەردوون بێکۆتا بێت، چونکە ئەگەر قەبارەیەکی دیارکراوی هەبێ، ئەوا لەخاڵێکی چەقەکەیدا هێزی کێشکردن وا دەکات گەردوون بتەپێتە نێو خۆی و هەرەس بهێنێت، کەواتە دەبێ بێکۆتا بێت.
بێکۆتا لە قەبارە و لە کاتدا بەردەوام دەخرێتە ڕوو، لەم دوایییانەشدا هەندێ جار دەکرێ هاوتای شتگەلە ڕاستەقینە فیزیکییەکان بە ئەزموون بوونەکەی بسەلمێندرێت، لە نموونەی ئەو ئەلیکترۆنانەی لە بۆشاییدا دەگۆڕدرێن بۆ دوو فۆتۆن، پاشان ئەم دووانەش دەبنە ماددە و دژە ماددە بە بەریەککەوتنیان یەکدی لەناو دەبەن و بڕێک وزە بەرهەم دەهێنن بەشێوەی دوو فۆتۆن و دەبنەوە بە ماددە و دژە ماددە و ... و بێکۆتا و هەتاهەتایە.
زاناکان ژمارەیەکی زۆریشیان دەڵێن، هەر دەمێک گەیشتنە ئاستی بێکۆتا لە بڕە فیزیکییەکان، ئەوا گریمانە و بیردۆزە زانستییەکانمان هەڵەن و پێویستە پێیاندا بچینەوە، یاخۆ هەمواریان بکەینەوە، یانیش بەلاوەیان بنێین. بۆیە لەبارەی گەردوونەوە لە بیردۆزی تەقینەوەی مەزن (Big bang)، خاڵی سفڕ، یان تاکایەتییان (Singularity)، پێ ڕاست نەبوو کە هەموو شتێکی هاوشێوەی چڕی و گەرمیی تێدا دەبێتە بێکۆتا، لەبەرئەوەی بیردۆزی ڕێژەیی گشتی ئەینشتاین و یاسا فیزیکییە گەردوونییەکان لەو ڕەهەندە بچووکانەدا کاریان پێ ناکرێت.
کێشەیەکی دیکەی بێکۆتا لە فیزیادا ئەوەیە، ئایا ئەو گەردوونەی ئێمە هەرهەبووێکی بێکۆتایە لە ڕابردوودا، یانژی سەرەتای هەیە، هەتاهەتایە و بێکۆتاش دەمێنێت، یاخۆ کۆتایی هەیە؟ چەندان بۆچوون و گریمانەی زانستی هەن، چی بۆ بوون و سەرهەڵدانی گەردوون، چی لە سیناریۆکانی کۆتایی هاتنی گەردوون کە پێ دادەگرن لەسەر ئەوەی گەردوون هەرهەبووەکی بێکۆتایە، لەبەر بوونی ڕێژە لەڕادەبەدەرەکەی وزەی تاریکیش، لەو ڕایەدان گەردوون بە هەمیشەیی و بێکۆتا فرەوانتر دەبێت.
هەر یەکێکیش زانیاری هەبێت لەسەر فیزیکی کوانتەم (Quantum mechanics)، ئەوە دەزانێت لە هەندێ بارودۆخدا دووچاری چەمکی بێکۆتا دەبینەوە، بەوەی ئێمە لە گەردوونێکین شتگەلەکانی ئەگەرەکیی و بێکۆتان، هاوکات لەو فیزیکەدا تێزی فرە گەردوونی و ژمارەیەکی بێکۆتا لە گەردوونەکانیش بوونی هەیە.
دەرەنجامی کێبڕکێکان
بێکۆتا بابەتێکی تێکهەڵکێش و ئاڵۆزە و ژمارەیەکی یەکجار زۆر کتێبی لەبارەیەوە هاتووەتە نووسین، هەر یەکێک بە جۆرێک لێکی دەداتەوە، بڕواهێنانی کەسەکان بە چەمکی بێکۆتا کاریگەری دەبێت لەسەر هزر و ڕەفتاریان بەرانبەر بە بابەتگەلە زانستییەکان، لەبەرئەوەشە زاناکانی ڕابردوو و ئەوانەی ئەم سەردەمەشمان، لە تێڕوانییان بۆ چەمکی بێکۆتا کێبڕکێ و ڕکابەرییەکی تووند لە نێوانیاندا بەرپا دەبوو.
لە کۆندا پیتاگۆراسییەکان (Pythagorisme)، هەرچەندە زیاتر هاوشێوەی کۆمەڵەیەکی ئاینی دەبیندران لەوەی زانستی بن، لەو باوەڕەدا بوون ژمارەکان دەست بەسەر گشت گەردووندا دەگرن و دیاردەکانی سروشت پێک دێن لە پێوەندییەکان و ڕێژە ماتماتیکییەکانی کە بە شێوەی ژمارە ڕاستەقینەکان بەدەر دەکەون، بەکورتی لەلای ئەواندا هەموو شتێک بەگوێرەی یاسا و ڕێسا ماتماتیکییەکان بەڕێوە دەچێت. کاتێکیش فەیلەسووف و ماتماتکیزان هیپسوس (Hippasus)، بە بەکارهێنانی بیردۆزی پیتاگۆراس لە سێگۆشەیەکی گۆشە وەستاوی دوو لای یەکسانی بە درێژی 1 سانتیمەتر، دەگاتە ئەو دەرەنجامەی کە درێژی ژێی سێگۆشەکە دەبێتە ڕەگی ژمارە 2، ئەو ژمارەیەش دوای کۆما زنجیرەی ژمارەکانی بێکۆتا درێژ دەبێتەوە (....1.4142857)، واتە ژمارەیەکی ناڕێژەییە و ناتوانین بەشێوەی ژمارەیەکی کەرتیی بینووسین. بەم بیرۆکەیە توانی سەرجەم فەلسەفەکەی ڕێبازی پیتاگۆراسییەکان بهەژێنێت، ئەوانەی دەیان گوت، تێکڕای ژمارەکانی گەردوون ڕێکوپێک و سنووردارن. پیتاگۆراسییەکان وەک ئاماژەمان پێی دا، هەر لە بنچینەوە باوەڕیان بە شتگەلە ناڕێژەییەکان و بێکۆتاکان نەبوو، بۆیە لەبەر بوونی ئەو ڕقەیان هەندێک دەبێژن، هیپسوسیان فڕێ داوەتە ناو دەریا و خنکاوە، یاخۆ دووریان خستەوە بۆ دوورگەیەکی لاچەپ هەتا لەوێدا مرد.
جۆرج کانتۆری ئەم دواییانەش کە زانای داهێنەری گشت چەمک و بنامەیەکانی بێکۆتایە، ئەو دەمەی لەبارەی بێکۆتا بیروڕاکانی خستە ڕوو، کەسانێکی زۆر و ژمارەیەک لە زانا ناودارەکانیش وەک پۆینکارێ (Henri Poincaré)، هێرشێکی تووندیان کرد سەر و بە شێت و تووشبوو بە نەخۆشی دەروونی ناوزەدیان کرد. بەهەمان شێوە زانای ماتماتیکی كرۆنێكەر (Leopold Kronecker)، دەی گوت، کانتۆر جادووگەرە و ئەو شتانەی لێیان دەدوێت فەلەسەفەیەکی بەتاڵن و دوورن لە ماتماتیک. بەداخەوە ئەمانەش بوون وایان لێ کرد، کانتۆر دووچاری نائومێدی و خەمۆکییەکی سەخت و نالەبار ببێت و بخرێتە ژێر چاودێری لە نەخۆشخانەی نەخۆشانی دەروونی.
کەچی لەگەڵ هەموو ئامانەش دوا جار بینیمان کە بیرۆکەکانی کانتۆر سەرکەوتنیان بەدەست هێنا، ئەمڕۆکە لە تێکڕای فێرگە و زانکۆکانی جیهان دەخوێندرێن، سەرجەم زانا هاوچەرخەکان کارەکانی بەرز دەنرخێنن.
دەکارین ڕای زاناکان لەو دێڕەی هیلبەرت کورت بکەینەوە کە دەبێژێت: "کەس ناتوانێت چیدیکە لەو بەهەشتە دەرمان بکات کە جۆرج کانتۆر بۆی دروست کردین".
تایبەتمەنییەکانی بێکۆتا؛
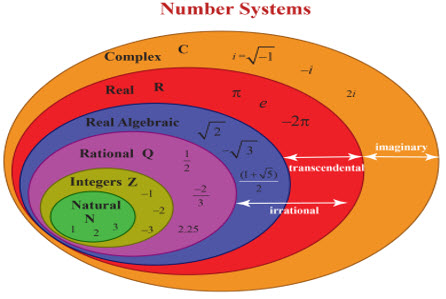
ناوی کۆمەڵەی ژمارەکان:
کۆمەڵەی ژمارە ئاڵۆز، یاخۆ ئاوێتەکان (Complex numbers)
کۆمەڵەی ژمارە ڕاستینە، یان ڕاستەقینەکان (Real numbers)
کۆمەڵەی ژمارە ناڕێژەیییەکان (Irrational numbers)
کۆمەڵەی ژمارە ڕێژەیییەکان (Rational numbers)
کۆمەڵەی ژمارە تەواوەکان (Integers)
کۆمەڵەی ژمارە سروشتییەکان (Natural numbers)
بڕە بێکۆتاکان:
- کۆی دوو بێکۆتای ئەرێنی، یان زیاتر یەکسان دەبێت بە بێکۆتای ئەرێنی ∞ + ∞ = ∞.
- کۆی دوو بێکۆتای نەرێنی، یان زیاتر یەکسان دەبێت بە بێکۆتای نەرێنی -∞ + -∞ = -∞.
- لێکدانی دوو بێکۆتای ئەرێنی، یان زیاتر یەکسان دەبێت بە بێکۆتای ئەرێنی ∞ × ∞ = ∞.
- لێکدانی بێکۆتای ئەرێنی لە بێکۆتای نەرێنی یەکسان دەبێت بە بێکۆتای نەرێنی -∞ × ∞ = -∞.
- لێکدانی دوو بێکۆتای نەرێنی، یەکسان دەبێت بە بێکۆتای ئەرێنی -∞ × -∞ = ∞.
- لێکدانی بێکۆتا لە ژمارەیەکی ناسفری یەکسان دەبێت بە بێکۆتا ∞ × أ = ∞.
- دابەشکردنی بێکۆتا بەسەر ژمارەیەکی ناسفری یەکسان دەبێت بە بێکۆتا ∞ ÷ أ = ∞.
- دابەشکردنی ژمارەیەکی ڕاستەقینە بەسەر بێکۆتا (تەنیا لە ژمێرەکردنە بێکۆتاکاندا) یەکسان دەبێت بە سفر أ ÷ ∞ = 0.
بڕە نەزانراو، یاخۆ نادیارکراوەکان:
- لێک دەرکردنی دوو بێکۆتای ئەرێنی دەبێتە بڕێکی نەزانراو ∞ - ∞ = نادیارکراو.
- کۆی بێکۆتای ئەرێنی و بێکۆتای نەرێنی دەبێتە بڕێکی نەزانراو -∞ + ∞ = نادیارکراو.
- لێکدانی بێکۆتای ئەرێنی و سفر دەبێتە بڕێکی نەزانراو 0 × ∞ = نادیارکراو.
- لێکدانی بێکۆتای نەرێنی و سفر دەبێتە بڕێکی نەزانراو 0 × -∞ = نادیارکراو.
- دابەشکردنی بێکۆتا بەسەر سفر دەبێتە بڕێکی نەزانراو ∞ ÷ 0 = نادیارکراو.
- دابەشکردنی بێکۆتا بەسەر بێکۆتا دەبێتە بڕێکی نەزانراو ∞ ÷ ∞ = نادیارکراو.
- دابەشکردنی ژمارەیەکی ڕاستەقینە بەسەر بێکۆتا (ئەگەر لە ژمێرەکردنە بێکۆتاکاندا نەبێت) دەبێتە بڕێکی نەزانراو أ ÷ ∞ = نادیارکراو.
- بێکۆتا بەرز بکرێتەوە بۆ توان سفر دەبێتە بڕێکی نەزانراو ∞^0 = نادیارکراو.
- ژمارە 1 بەرز بکرێتەوە بۆ توان بێکۆتا دەبێتە بڕێکی نەزانراو 1^∞ = نادیارکراو.
........................
سەرچاوەکان؛
نووسەرەکان خۆیان بەرپرسیارێتی وتارەکانی خۆیان هەڵدەگرن، نەک کوردستانپۆست